
Developing a Dungeon-Building algorithm has been a personal project for quite a while, but I've always spent more time writing the code than thinking of the theory. Unsurprisingly, I ended up writing inefficient, boring tunelling algorithms.
In this blog post, we will dive into the subject and try to develop a new idea, from the theory to the implementation in C.
Goals
The algorithm should generate random maps suitable for a Roguelike game. Generated maps should not necessarily be composed of interconnected rooms like NetHack does: They could also look like caverns or mines, e.g. the ones used in Cavern or Possession.
suitable for a roguelike game means that generated maps should be connected (connected as in graph theory: each point of the map should be accessible to the player).
Furthermore, the algorithm should be scalable (it should work fine on low power devices but should also take advantage of more powerful machines) and modular (it should be possible to generate a variety of maps using the same code base).
First idea
function fill_map(Map* map, Float filling_coefficient, Float room_size):
fill map with empty characters
Point point
do
point = select point at random in the map
while !is_suitable_initial_point(map, point)
Integer filled = 0
do
filled += generate_room(map, &point, max_room_size)
while filled < filling_coefficient * map.size
function generate_room(Map* map, Point* point, Float room_size):
// Used as a black box. It should:
// Generate a rectangular room in passed map around passed point. Return
// the number of points newly marked in the map. Select coordinates in
// generated room and update point.
// Also, room doesn't have to be rectangular, it can have any shape as
// long as it is random
function is_suitable_initial_point(Map* map, Point initial_point):
if initial_point.y < 1 or map.height - initial_point.y <= 1 or
map.width - initial_point.x <= 1 or initial_point.x < 1:
return false
return true
This algorithm chooses coordinates in the empty map and uses them as initial point to generate a room. Then, as long as the desired size isn't reached, new coordinates are chosen in the previously generated room and used as initial point to generate another room, so on and so forth.
Suitability
Any map generated in this way is necessarily connected since we always choose the next initial point in the previously generated room. It is inplace because we don't need any buffer, which is a very interesting quality for embedded devices.
Also, we can be sure that the algorithm ends. In fact, as long as the desired size is smaller than the map, there will always be 'enough place to fill', and even if the algorithm may loop some time over previously marked points, it will always 'find' the remaining unmarked coordinates. I didn't try to find its worst case bound, but it could be interesting to do it.
Implementation
I have implemented the algorithm in C for the following reasons:
- I want to use the generator for Arduboy games, which limits the choice to C and C++.
- In my opinion, object oriented programming doesn't bring anything interesting here. The algorithm is pretty straightforward and I except to write something more efficient in C than in C++.
I have written two generate_room() functions which allow the generation
of rectangular and elliptic rooms.
The implementation is certainly perfectible, but for the moment it does the job in a sufficiently efficient way. You can find the source code on GitHub.
Some examples
You can find some examples of generated maps here, with different parameters.
Complexity and speed
The arguments of the fill_map function are interesting for modularity and
scalability.
room_size allows control over the maximal size of generated rooms. Small
values will produce fine-grained maps, at the cost of a higher computational
overhead (more loop cycles are required to achieve the desired filling).
On the other hand, the filling_coefficient variable allows control over the
map's filling (for example a filling coefficient of 0.9 will produce a map which
will have at most 10% of empty space).
Together, these two parameters allow to generate maps with a pre-defined filling lower bound
regardless of the available hardware, with room_size being the variable parameter. Please
note that high values of room_size do have an impact on the final result. We will discuss this point later.
The following chart represents the average number of CPU cycles needed to
generate a map, in relation to the value of room_size (with filling_coefficient
constant 0.4).
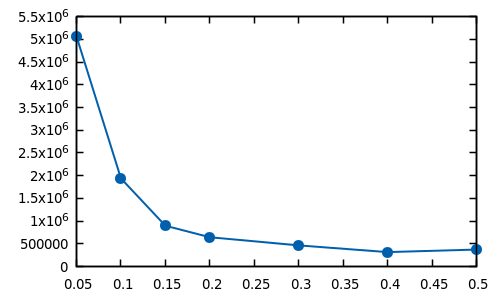
As you can see, the computational overhead increases exponentially as room_size
approaches zero. This is because the probability that a newly generated room is
fully included in the already filled space is higher when room_size is small.
Room size upper bound and final result
So, the room size upper bound has an impact on the computation costs, but what is its impact on the final result ?
In fact, running the current C implementation with room_size = 0.05 on modern
personal computers is fast (1-2ms in average with a core i5-5200U). On (very?)
low power devices however, the higher computational overhead might be a
problem. For that reason, it would be a good idea to study the effects of
room_size on the final result, in order to maximize it and make
computation costs as small as possible with the best map quality possible.
Statistical experiment shows that higher values of room_size imply:
- more big rooms (trivial)
- increased impact of
generate_room()on the final result (less trivial) - poorer (less natural) result when mixing several room generators
Lessons I learned from the C implementation:
- elliptic room generators should be preferred for natural results with high
values of
room_size. - rectangular room generators might be of interest with high values of
room_sizebut results are less predictable and very big rooms may be problematic because more frequent.
These results are of course only experimental and potentially subjective. Interested users may have to play around with the parameters to find the most appropriated ones for their specific usages.
You can find some result examples here with the algorithm using only rectangular/elliptic room generators.
Other ideas
In the end, this algorithm works well. It is fully usable and produces very nice
results for small values of room_size. generate_room() may be studied
further to find optimal solutions, but this is not critical as long as the
implementation is run on modern hardware.
I'm probably going to work on other blog posts about random map generation. I think it is a very interesting subject and I have other ideas I'd still like to develop. For example, I've thought of generating a big map and then randomly removing parts of it until we reach the desired size.
In this case it would be fairly easy to guarantee the connection property, since the map can be represented as a graph, with each coordinates being a node: Using graph theory we can make sure that removing a node won't dis-connect the graph, for example by removing leaves of its spanning tree.
This algorithm would have a linear worst case bound.
Credits & further reading
I have used Valgrind and kcachegrind as profiling tools.
Some interesting links:
- Procedural Content Generation Wiki: Dungeon Generation
- Memory optimization: The Lost Art of C Structure Packing
Heading image from Wikimedia Commons.